Fixing Boundary Violations

4.3 Simulation Results

Table 1 presents the results of three simulation tests. The TRM model generates admissible solutions by 35.5%, 11.4%, and 30.6% in the three simulations, while the solutions of the TRMCO model are all 100% admissible. The lower percentage of the second simulation for the TRM model is associated with the serious boundary violation by the designed sampling scheme. Apparently, the TRMCO model is more reliable and not subject to the problem of nonlinearity or multicollearity.

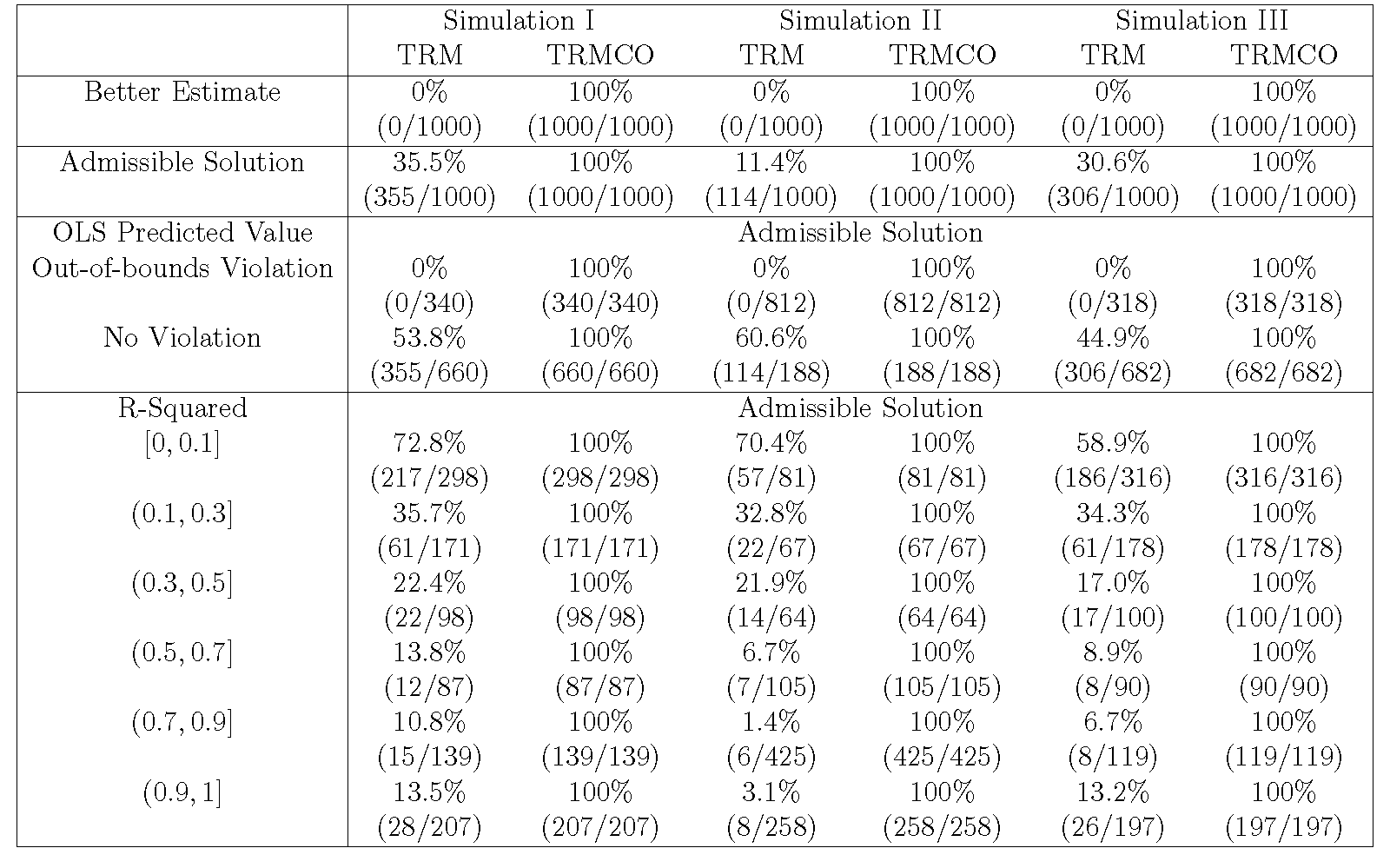
Table 1 Simulation Results for the TRM and TRMCO model

When we consider which method performs better in parameter estimation, the TRMCO model has a better estimate (admissible solution $+$ greater loglikelihood) for 100% in all three simulations. Again, this result indicates the superiority of the TRMCO model. Breaking down the cases by the OLS out-of-bounds violation, we find that the TRM model cannot correct boundary violations at all (0%), but the TRMCO model is capable of doing so (100%). Regarding those cases that do not have the OLS out-of-bounds violation, the TRM model only has admissible solutions in 53.8%, 60.6%, and 44.9% for the three simulations, while TRMCO has no instances of boundary violations.

Another key factor in the sampling scheme is the degree of explanatory power. We break down the cases by different r-squared measures into six categories: [0,0.1], (0.1,0.3], (0.3,0.5], (0.5,0.7], (0.7,0.9], (0.9,1]. The result consistently shows that the TRMCO model performs in an unconditionally superior fashion (100% admissible solution), regardless of r-squared, nonlinearity, and multicollinearity. With regard to the TRM model, the performance quickly worsens if r-squared is larger than 0.1. The successful rate for admissible solutions when r-squared is smaller than 0.1 is 72.8%, 70.4%, and 58.9% for the three simulations, respectively. It is reduced to less than 40% when r-squared is between 0.1 and 0.3 and, continues dropping to 20% when r-squared is between 0.3 and 0.5, and finally falls below 15% when r-squared is above 0.5.

Regardless of the superiority of the TRMCO model, it is informative to understand the difference in the solutions from both methods. Table 2 crosstabulates the mean absolute deviation of the estimates ($\hat{\beta}_{0}$,$\hat{\beta}_{1}$,$\hat{\beta}_{2}$,$\hat{\sigma}$) for the TRM model, by using the TRMCO solution as the default answer. The result indicates very little difference between all parameter estimates when the solution of the TRM model has no boundary violations. The mean absolute deviation of the parameter estimates is at most $0.001$ and is almost negligible. On the other hand, when the TRM model fails to generate an admissible solution, the margin of difference is significantly larger, particularly when the multicollinearity is high, except for the scale parameter $\sigma$.

The mean absolute deviation of the $t$ statistic can provide further information regarding the sensibility of the hypothesis testing results. As Tables 2 shows, ${{t}_{{{\beta }_{0}}}}$, ${{t}_{{{\beta }_{2}}}}$, and ${{t}_{\sigma }}$ have milder variability when the solution of the TRM model is admissible. However, the variability significantly increases when the TRM model has boundary violations, regardless of different sampling schemes. This result indicates that hypothesis testing can be greatly affected if the TRM fails to find an admissible solution. Note that ${{t}_{{{\beta }_{1}}}}$ does have little variability in all three simulations since $x_{1}$ and $y$ in the sampling scheme are supposed to be independent (Simulation I and II) or highly collinear to $x_{2}$ (Simulation III). Given that little explanatory power is designed to $x_{1}$, the variability is marginal.

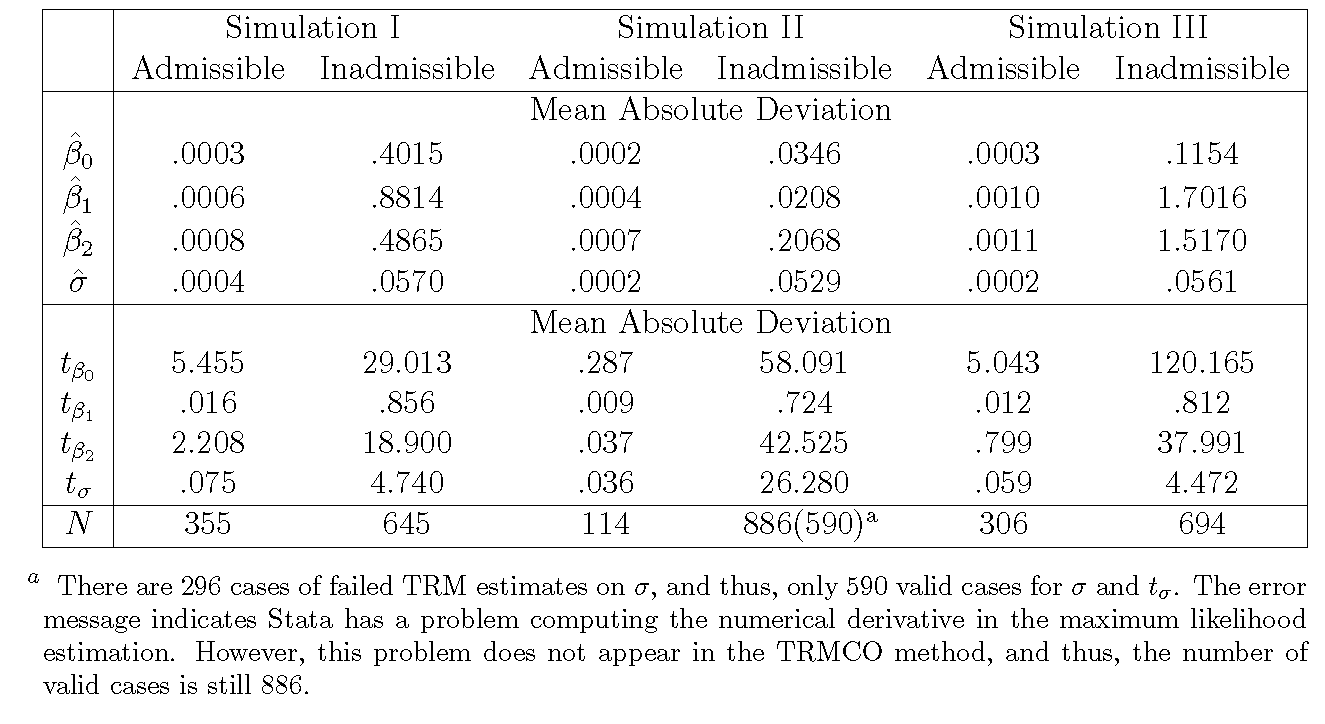
Table 2 Comparison of the Parameter Estimates

Some cases of the TRM model suffer from the problem of negative variance. All of these cases occur in Simulation II in which the strong nonlinear logit relationship is assumed between $x_{2}$ and $y$. This result indicates that negative variance becomes a serious problem for the TRM model when the boundary violation is extreme.¹⁴ As Table 2 shows, the TRM model generates negative variance in 33.4% (296/886) of the cases when it fails to find an admissible solution. This reflects the weakness of the TRM model in handling data for which the linear assumption has been significantly violated.

Although the difference of the TRMCO and TRM models is limited when the latter solution has no boundary violations, the weakness of handling various data properties, such as varying explanatory power, nonlinearity, and multicollinearity, as well as the problem of negative variance, all makes the TRM model highly unreliable. Thus, the overall findings of the three simulation tests consistently suggest that the TRMCO model is superior to the TRM model.

____________________

Footnote

¹⁴When ceiling or floor effects are very strong, negative variance happens and this indicates strong violation of the linear specification of the regression model. (Kolenikov and Bollen, 2012, 6)